A Random Walk Down Monopoly Lane

Since my Candyland post seemed to get a good response, I thought I'd take a stab at a few other games everybody knows. "How about Monopoly?", I thought. [Let's do this right at least once: it's Monopoly®.] A small amount of research revealed a wealth of material on probabilities of landing on each square, expected incomes, expected payback times, probability of landing in jail and much much more. Most of those links take you to the superb Probabilities in the Game of Monopoly page by Truman Collins. Since Truman and others have already done such a good job on this topic, and I already discussed the idea of a Markov chain earlier, I decided I needed a different angle on this game.

Describing the probabilities of landing on each square as a Markov process is useful information, and you might easily use that to improve your play, but it doesn't describe the actual progress of the game. Unlike Candyland, Monopoly isn't about what square you are on and getting to the end, it's about accumulating wealth. ALL the wealth. A full description of how this works in Monopoly would be quite long, but we might learn a bit by constructing a much simpler sort of game which just keeps track of wealth.

Consider a game where two players, call them P1 and P2, start with equal amounts of money, and each turn they trade some random amount of money to the other player. If we think about the difference in wealth between Players 1 and 2 (P1 $ minus P2 $), and plot this value over a series of turns, it might look something like this (to right). Here I set up a spreadsheet where each player randomly gives the other player between $0 and $19 each turn. This sort of series is known as a Random Walk.

Here is another plot with ten similar random walks. In these instances P1 is behind P2 in wealth at turn 200 (the difference is negative) more often than not. This just random variation, and if we looked at many such plots, we expect should expect that P1 will be winning (wealthier than P2) 50% of the time. In this respect the game is fair; it is completely random and no player has any advantage.

"Now what?", you say. I created a really boring game that no one would ever play. Let's make the game, which I will now refer to as "Monopoly-Walk", a little more complicated by adding or changing some rules that make it a little bit more like the original Monopoly:

1) Let each player start with $2000.
2) Let each player gain $20 per turn.
3) On each turn both players randomly give each other a randomly determined amount of money between 0% and 6% of the other player's wealth.
4) When one player controls all the wealth, the game is over.

Rules #1 and #2 are similar to Monopoly; each player starts with equal wealth, and gain wealth over time. My version has a fixed income every turn for simplicity.
Rule #3 is our random walk, but this time it's different, because if one player gains greater wealth the other will probably end up paying them more money. Neither player starts with any advantage, but sooner or later one player gains a big advantage. This is a big simplification from the original game, but it still captures the essential element of Monopoly: THE RICH GET RICHER.
Rule #4 is identical to our original Monopoly game.

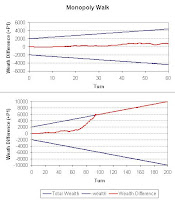
So here are two plots of a game of Monopoly-Walk. These are identical plots, just a different time scales to better show what is going on. This "walk" (red line) looks much smoother than the random walks above, but the scale on the y-axis is much greater and so the difference do not look as jagged. The blue "cone" line represents the total wealth in the game (or maximum difference in wealth) as both positive and negative values. When the red line touches one of the blue, the game is over and one player has won (P1 is the difference is positive, P2 if it is negative).
In this example the players are nearly equal in wealth for the first 60 turns (difference is ~0), but then player 2 gains a small advantage which eventually leads to a win about turn 125.

Here is the spreadsheet I used to create the plots: Monopoly2.xls. You can try adjusting the starting values and see how that changes the game (See my comments for more explanation). If you don't want to try that, here are some more plots you can look at to get a better idea what is going on.


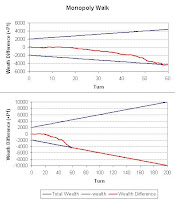
You can see here that the game usually remains somewhat "flat" at first, with no big swings in wealth. Later one, when one player has more than a tiny advantage, that advantage quickly translates into a win. Let's think a bit more about the remaining differences between this simple game and Monopoly. Monopoly has properties which must be purchased, thus reducing a player's wealth. The properties give small rent payments at first, but later on are developed (also reducing wealth) to allow greater rents, earning the owner a greater share of the other player's money on future turns. These things are a delaying effects between first acquiring wealth and turning that wealth into higher rents, and so the game remains essentially random for a longer time before one player gains a decisive advantage. Monopoly also has "taxes" that remove wealth from a player and the total wealth available in the game. This serves as another sort of delay to a player gaining that decisive advantage. These taxes also add additional randomness, making the game even less predictable. Add in three or more players and gentle random walk turns into a wild roller-coaster ride governed by luck and player moxie.

So that's my angle on the game Monopoly. I doubt it will help anyone play better, but it may allow the opportunity to appreciate a different sort of mathematical process, one that also happens to be a lot of fun.

PS: If one reader would try my spreadsheet and report success or failure, that would be appreciated.